Algunas características de este conjunto numérico son:
- El conjunto de los números naturales (
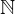 ) es el primer conjunto numérico construido y estudiado por el hombre. Se denota por
) es el primer conjunto numérico construido y estudiado por el hombre. Se denota por 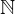 = {1, 2, 3, 4, … }.
= {1, 2, 3, 4, … }. - El conjunto de los números naturales es un conjunto con un primer elemento, ordenado e infinito.
- El conjunto de los números naturales, en sentido estricto, no contiene al cero; si se quiere incluir este elemento en el conjunto, se denota por
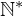 = {0, 1, 2, 3, … }, también es conocido como números cardinales y se puede escribir
= {0, 1, 2, 3, … }, también es conocido como números cardinales y se puede escribir 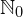 .
. - Los números naturales expresan el número de elementos que contiene un conjunto dado. Por ejemplo, el número natural 5 representa un conjunto formado por cinco elementos
Relación de orden
En el conjunto de los números naturales se pueden definir las relaciones de orden: menor que, mayor que o igual que. Es así que dado dos números naturales cualesquiera, siempre hay uno menor y otro mayor, salvo que ambos números sean iguales.
Símbolos para comparar
Los símbolos que utilizamos para comparar los numeros naturales son:
| Símbolos | Ejemplos |
|---|---|
| 2 9 8 |
|
Representación de los números naturales en la recta numérica
Los números naturales los podemos representar de forma ordenada en una recta numérica. En ella, un número que se encuentre a la derecha de otro será mayor que él.


Propiedades de los números naturales
En el conjunto de los números naturales se definen habitualmente dos operaciones, la adición y multiplicación. A continuación se presenta una tabla resumen de las propiedades y operaciones en ![]() .
.
| Op. / Prop. | Adición | Multiplicación |
|---|---|---|
| Clausura | Al sumar dos números naturales, su resultado también será un número natural.
|
Al multiplicar dos números naturales, su producto también será un número natural.
|
| Conmutatividad |
|
|
| Asociatividad |
|
|
| Elemento neutro | No se cumple. |
|
| Elemento inverso | No se cumple. | No se cumple. |
| Distributividad | Hace referencia al producto respecto de la suma, y no de la suma respecto del producto.
|
|
En el conjunto de los números naturales, las operaciones de sustracción y división se definen con algunas restricciones.
En la sustracción se debe cumplir que el minuendo debe ser mayor al sustraendo.
Ejemplos: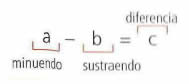
- 43 – 13 = 30, donde 30
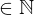
- 32 – 54, donde su diferencia
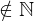 , pues el minuendo 32 es menor que el sustraendo.
, pues el minuendo 32 es menor que el sustraendo.
En la división, el dividendo debe ser múltiplo del divisor.
Ejemplos: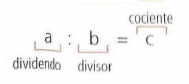
- 36 : 9 = 4,donde 4
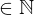 .
. - 27 : 4, donde su cociente
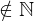 , pues el dividendo no es múltiplo del divisor.
, pues el dividendo no es múltiplo del divisor.
