Uno de los requisitos para iniciar con buen pie en el terreno matemático del álgebra es la comprensión de los componentes de un término algebraico, ya que es el conocimiento más elemental, que te permitirá progresar satisfactoriamente en la asimilación de esta hermosa rama de las matemáticas.
En el álgebra existen expresiones o códigos que sustentan todas las operaciones conocidas en esta rama, en general, estos son llamados términos algebraicos, y cuentan con una diversidad de formas, la más simple de ellas son los denominados monomios. Entender a los monomios te permitirá comprender expresiones algebraicas más complicadas como los binomios y los polinomios.
Esencialmente, los componentes de un término algebraico son: el signo, el coeficiente, la parte literal y el grado. Cada uno de estos componentes se te serán definidos e identificados en los siguientes párrafos.
Si hablamos de término algebraico, es necesario saber qué es un monomio
Como ya te mencionamos, los monomios son los términos algebraicos más sencillos con los que puedes toparte al hacer álgebra, y esto es porque son expresiones compuestas por un solo símbolo matemático. Este símbolo, formalmente, está dado por el producto de factores, es decir, constantes y/o variables, que tienen potencias positivas, enteras o ambas.
Para dejar el panorama completamente claro, te presentamos los siguientes ejemplos de un término algebraico (monomio):
Para el primer ejemplo, se puede apreciar fácilmente el producto (multiplicación) entre el número 5 (constante) y la letra d (variable), a pesar de que el signo *, de multiplicación, es omitido. Por lo que, cumpliendo la condición anteriormente mencionada, se tiene un monomio.
En el segundo ejemplo se tiene únicamente al número 2, el cual aunque es una constante únicamente, aprueba el concepto de monomio.
Para el siguiente caso tenemos otra simbología en juego. Tenemos un signo negativo y una variable elevada al cuadrado, sin embargo, se sigue cumpliendo con el concepto de monomio, conservándose una multiplicación de factores.
Por último, tenemos a primera vista un caso en el cual se produce multiplicaciones (en el numerador y denominador) seguidas de una división, por lo que podría decirse que no es un monomio. Sin embargo, hay que aclarar que el producto sí se da pero a la inversa, constituyendo un único término algebraico.
Componentes del monomio
Para dar a entender cuáles son los componentes de un término algebraico se tomara el ejemplo número 3, de los anteriores. Este ejemplo será la expresión clave para ir señalando cada una de las partes del término algebraico, aunque, adicionalmente se mostraran algunos ejemplos para afianzar las ideas.
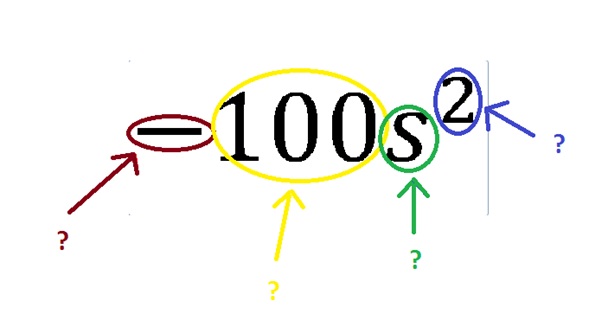
Signo de un monomio
Como muy bien se sabe de la aritmética, matemáticamente existen 2 signos, el mas (+) y el menos (-). Estos signos han de ser bastante conocidos, pues, son las claves para realizar operaciones como sumatorias y restas entre enésimas cantidades.
En términos físicos, se puede hacer una analogía: al igual que una partícula puede poseer carga positiva o negativa, los monomios presentan esta misma situación, es decir, una carga. Por lo tanto, según el signo, el término algebraico puede ser positivo o negativo.
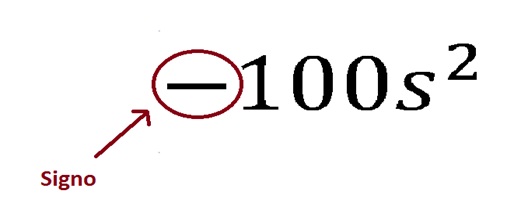
Para el caso del ejemplo principal seleccionado, se puede ver, sin ninguna complicación, que es una término algebraico de carga negativa, o simplemente, negativo, dejando a un lado la analogía física. Sencillamente, el signo que se encuentre por delante de la expresión es quien determinara si es positivo o negativo.
Para complementar, ejemplos de monomios positivos son los siguientes:
A pesar de que ninguno de los términos muestra un signo +, este es asumido ya que implícitamente está allí; por razones de formalismo matemático. La no presencia de un signo – delante del término algebraico conlleva una razón más clara de la implicación matemática; por inferencia.
Coeficiente de un monomio
Ahora seguimos con el coeficiente, que es el acompañante numérico de la variable, es decir, la constante. Recordando lo anterior, tenemos que en un monomio se da un producto entre constantes y/o variables.
Por regla general, el coeficiente es el primer factor de un término algebraico, tomando en cuenta el signo de la expresión.
De esta forma, tenemos que para nuestro ejemplo principal el coeficiente del monomio es el -100.
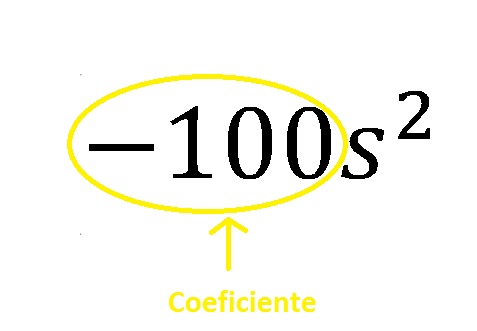
Adicionalmente, te mostramos los siguientes ejemplos para consolidar el concepto del coeficiente algebraico:
Para el primer ejemplo, se tiene que el 8 es el coeficiente. Y por último, se presenta un coeficiente racional y negativo, el -3/4.
Parte literal del monomio
Ya tratado el elemento constante de un término algebraico, es preciso pasar a considerar ahora a la parte variable o literal. Esta parte literal está constituida por las letras del monomio.
En el ejemplo principal que hemos tomado la parte literal es la letra s^2, único elemento alfabético presente en el término algebraico. Se considera el exponente de la variable, ya que la potenciación implica la presencia de una segunda variable en la expresión, por lo que en realidad hay 2 partes literales, las cuales son iguales.
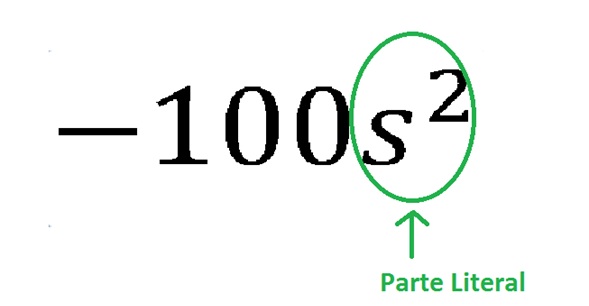
Auxiliarmente, te traemos los siguientes ejemplos para aclarar la idea expresada:
Para nuestro primer ejemplo, evidentemente la variable z es la parte literal. Para el segundo, aunque aparentemente es una expresión complicada, la parte literal está dada por la relación de:
![]()
Todas las letras junto con sus exponentes.
Grado del monomio
De todos los componentes de un término algebraico o monomio este es que requiere mayor atención, puesto que puede ser absoluto o con relación a una letra.
El grado absoluto se define como la sumatoria de los exponentes de las partes literales del monomio. En cambio, el grado con relación a una letra está dado por el exponente de la parte literal referenciada.
Continuando con nuestro ejemplo principal, debido a que el término algebraico contiene una sola parte literal, es un monomio de segundo grado.
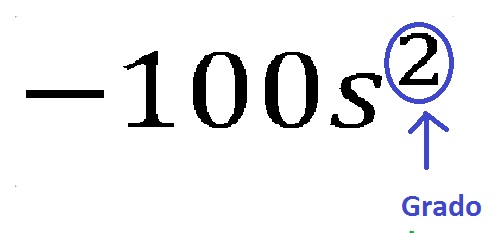
Como complemento, conviene exponer algunos ejemplos, de mayor complejidad que el principal considerado, los cuales son los siguientes:
El grado absoluto del primer ejemplo está dado por la suma de 1 y 3; exponentes de las variables, siendo de cuarto grado. El monomio es de primer grado con relación a x, y de tercer grado con relación a y.
Por último, tenemos que el grado absoluto del segundo término algebraico mostrado es de sexto grado. En contraste, es de primer grado con relación a d, de segundo grado con relación a c, y de tercer grado con relación a w.
Ejercicios propuestos para identificar a los componentes de monomios
Para finalizar, te dejamos algunos términos algebraicos para que ejercites tu mente y pongas a prueba los conocimientos matemáticos adquiridos. De esta forma, identifica el signo, el coeficiente, la parte literal y el grado (absoluto y relativo) de las siguientes expresiones:
