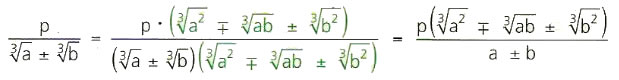Racionalizar una expresión fraccionaria con raíces inexactas en el denominador (números irracionales) consiste en obtener otra expresión fraccionaria equivalente, pero sin que aparezcan raíces en el denominador.
Las siguientes expresiones fraccionarias tienen números irracionales en el denomirnador:
¿Para qué racionalizar?
Una de la razones por las cuales se racionaliza es para realizar la división, ya que el divisor no puede ser un número irracional.
Para racionalizar se debe amplificar la expresión por algún factor que permita expresar el denominador sin raíces (como un número racional).
Racionalización de expresiones de la forma 
Para racionalizar expresiones de la forma se debe amplificar por el factor
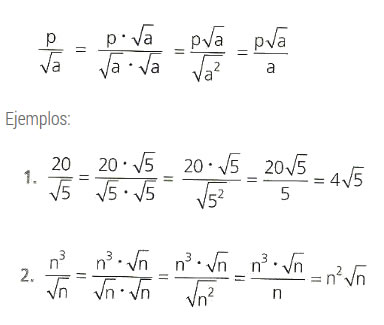
Racionalización de expresiones de la forma ![\frac{p}{\sqrt[n]{a^{k}}}](https://chart.apis.google.com/chart?cht=tx&chl=%5Cfrac%7Bp%7D%7B%5Csqrt%5Bn%5D%7Ba%5E%7Bk%7D%7D%7D%20%20%20%20%20%20)
Para racionalizar expresiones de la forma
se debe amplificar por el factor

Racionalización de expresiones de la forma 
Para racionalizar expresiones de la forma
se debe amplificar por el factor
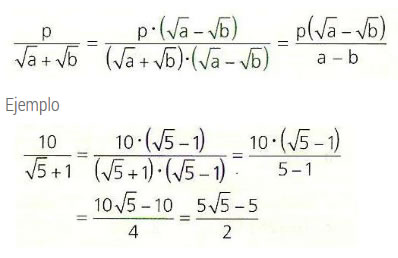
Para racionalizar expresiones de la forma
se debe amplificar por el factor
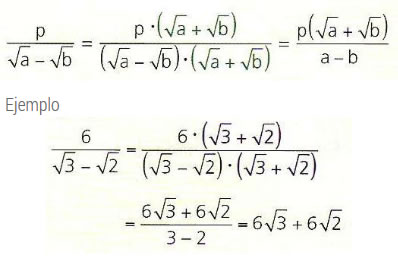
Racionalización de expresiones de la forma ![\frac{p}{\sqrt[3]{a}\pm\sqrt[3]{b}}](https://chart.apis.google.com/chart?cht=tx&chl=%5Cfrac%7Bp%7D%7B%5Csqrt%5B3%5D%7Ba%7D%5Cpm%5Csqrt%5B3%5D%7Bb%7D%7D%20%20%20)
Para racionalizar expresiones de la forma se debe amplificar por el factor