Término algebraico

A continuación definimos qué es un término algebraico desde tres principios fundamentales del álgebra:

Un término algebraico es el producto de un factor numérico por una o más variables literales.
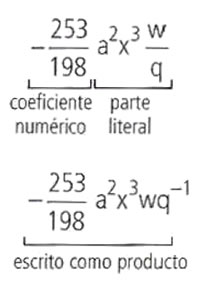
En cada término algebraico se distinguen el coeficiente numérico (que incluye el signo y constantes matemáticas) y la parte literal (que incluye variables).
Se define el grado de un término algebraico como la suma de los exponentes de cada factor de la parte literal.

Ejemplos:

Término algebraico	Coeficiente numérico	Parte literal	Grado
$a^{3} b c$	$1$	$a^{3} b c$	$3+1+1=5$
$5^{12}m ^{3}n ^{a}$	$5^{12}$	$m ^{3}n ^{a}$	$3+a$

Expresiones algebraicas

Una expresión algebraica es la suma de dos o más términos algebraicos.
De acuerdo con el número de términos que componen una expresión algebraica, estas se clasifican en: monomios (un término) y multinomios (dos términos o más). A los multinomios con dos términos se les llama binomios, y los de tres términos, trinomios.
Si los exponentes de la parte literal son todos positivos, llamaremos a la expresión algebraica polinomio.

Término algebraico

Ejemplo:

Monomios	Binomios	Trinomios	Multinomios
$b$	$a ^{2}-b ^{2}$	$m ^{2}+ 2mn-n ^{2}$	$a ^{3}+c+4a ^{3}+c ^{2}$

El grado de una expresión algebraica corresponde al mayor de los grados de los términos que la componen.

Ejemplo:
Los términos del multinomio

$x ^{3}y ^{2}z ^{9}-5x ^{2}yz ^{8}+\frac{x^{15}y}{z}$

tienen grados $14$ , $11$ , y $15$ , respectivamente. Luego, el grado del multinomio es $15$ .

Valoración de expresiones algebraicas

Valorar una expresión algebraica consiste en asignar un valor numérico a cada variable que aparece en la expresión y resolver las operaciones aritméticas que correspondan para obtener el valor numérico final de la expresión.

En ciertas situaciones interesa conocer el exponente de una variable en particular dentro de un término o una expresión algebraica. Se define el grado de un término algebraico con respecto a una letra como el exponente de esa letra. Análogamente, el grado de una expresión algebraica con respecto a una letra es el mayor de los grados de cada término con respecto a esa letra. Así, el grado de $ab^{2}c^{3}d$ con respecto a $b$ es $2$ y con respecto a $d$ es $1$ . Mientras que el grado de $4x ^{2}y ^{2}-3x ^{3}+xy ^{5}$ , con respecto a $x$ es $3$ y con respecto $a$ y es $5$ .

Aspectos adicionales de la nomenclatura algebraica

Además de todo lo mencionado anteriormente, debes de saber que las principales expresiones del álgebra, es decir, los términos algebraicos (monomios) y los polinomios, tienen una clasificación completamente particular, aunque mayormente similar, que permite diferenciar y comprender diferentes expresiones. De esta manera, serás capaz de reconocer cuando efectuar ciertas operaciones, así como algunas simplificaciones para reducir la expresión algebraica.

Debido a que queremos exponerte todo el panorama detrás de los términos algebraicos a continuación te explicaremos en qué consiste los aspectos adicionales del arte de las generalizaciones.

Clases de términos algebraicos

Principalmente, vamos a abordar la clasificación de la expresión algebraica más simple, estos son, por supuesto, los monomios o los términos algebraicos. Existen los siguientes:

Término entero: son aquellos monomios que no tienen una parte literal como denominador, por ejemplo:

$10b^{2}$
$\frac{4cd^{2}}{7}$

Término fraccionario: a diferencia de los anteriores términos algebraicos, estos sí tienen partes literales como denominadores. Ejemplos de términos fraccionario son:

$\frac{2a}{c}$
$\frac{ab^{2}c^{3}}{d^{4}e^{5}f^{6}}$

Término racional: son todos aquellos que no poseen radicales. Dentro de esta clasificación se encuentran todos los ejemplos previos.
Término irracional: como lo puedes adivinar, se les llama irracional a todo término que tiene un radical. Algunos ejemplos de términos algebraicos irracionales son los siguientes:

$sqrt{b}$
$\frac{\sqrt[4]{5xy}}{6a}$

Términos homogéneos: así llamados por poseer el mismo grado absoluto, por ejemplo:

$2a^{3}b y \frac{a^{2}b^{2}}{9}$
$\frac{m^{4}n^{6}p^{10}t^{3}}{46} y \frac{25m^{5}n^{5}p^{9}t^{4}}{78}[\latex]</li> </ol> Haciendo ejercicio mental con lo que hemos aprendido del grado absoluto de <strong>términos algebraicos</strong> podemos ver que el grado absoluto de los monomios del primer ejemplo es igual a 4, coincidiendo en ambas expresiones. Lo mismo volvemos a comprobar en el segundo ejemplo, en el que la homogeneidad se da por el grado absoluto de 10. Y por último, tenemos términos homogéneos de grado absoluto 23. <ul> <li>Términos heterogéneos: estos términos la otra cara de la moneda, la contraparte, de los términos homogéneos. Por ello, el grado absoluto de los términos comparados es diferente. Aquí tienes unos <strong>ejemplos de términos algebraicos</strong> heterogéneos:</li> </ul> <ol> <li>[latex] 2a y 55a^{3}$
$\frac{xy^{2}}{5} y \frac{2xy^{3}}{5}$

Con estos 2 ejemplos podemos ver fácilmente como los monomios difieren en grado absoluto. En el primer ejemplo el grado absoluto del primero es 1, mientras que el segundo monomio tiene grado 3. En el segundo ejemplo, se verifica nuevamente una heterogeneidad, el primer término tiene grado absoluto de 3, y el segundo término, un grado absoluto de 4.

Clases de polinomios

Así como los términos algebraicos, las expresiones más simples, tienen una clasificación según ciertas condiciones numéricas, los polinomios, las expresiones más complejas, también cuenta con su propia clasificación. Esta clasificación es bastante parecida a la que fue explicada, por lo que no tendrás ningún tipo de complicación para entenderla.

Polinomio entero: polinomio en el cual ninguno de sus términos tiene una parte literal como denominador, como estas expresiones:

$a^{2}+2b^{3}+3c^{4}[\latex]</li> <li>[latex]x^{2}+2xy+y^{2}$

Polinomio fraccionario: es aquel compuesto por términos algebraicos con denominadores literales, por ejemplo:

$\frac{a}{b}-\frac{c}{b}+\frac{d}{e}$
$\frac{x^{2}}{y}+\frac{z^{2}}{w}$

Polinomio racional: polinomios que no contienen términos radicales. Dentro de esta clase entran todos los ejemplos de polinomios anteriores.
Polinomio irracional: polinomios que cuentan con términos radicales, como por ejemplo:

$sqrt{a}+sqrt{b}+sqrt{c}$
$2a*sqrt{xy}-3b*sqrt[3]{z}+5cd*sqrt[4]{wt}$

Polinomio homogéneo: polinomio con términos de igual grado absoluto. Algunos ejemplos son estos:

$a^{2}+2ab-b^{2}$
$x^{4}+2x^{3}y+3x^{2}y^{2}-5xy^{3}-7y^{4}$

Polinomio heterogéneo: representa el contraste del polinomio anterior, puesto que el grado absoluto de sus términos algebraicos es diferentes. Aquí algunos ejemplos:

$x^{2}+2x+4$
$y^{3}+3x^{2}y^{2}+5yx^{5}+7x$

Polinomio completo: se dice que un polinomio es completo con relación a una letra cuando contiene todos los exponentes sucesivos de esta parte literal, desde el más alto al más bajo. Ejemplos de términos algebraicos pertenecientes a esta clasificación son estos:

$x^{4}-x^{3}+x^{2}-x$
$y^{3}+xy^{2}-x^{2}y+x^{3}$

En el primer ejemplo, tenemos un polinomio completo en relación a x. Y, para el segundo, tenemos un polinomio completo con relación a y y x.

Polinomio ordenado: la ordenación de los polinomios se da en relación a una letra, denominándosele letra ordenatriz. Para esta clase de polinomios se toma en cuenta la ascendencia o descendencia de los exponentes. Fijémonos en estos ejemplos:

$-4z^{3}+z^{2}-5z$
$2w^{5}+3w^{4}u-5w^{3}u^{2}+11w^{2}u^{3}-13wu^{4}+17u^{5}$

La letra ordenatriz del primer ejemplo es la z, estableciendo una ordenación descendiente. Para el segundo ejemplo, tenemos 2 letras ordenatrices. Con respecto a w, la ordenación del polinomio es descendiente, y con respecto a u, la ordenación es ascendente.

Operaciones básicas con términos algebraicos

Al igual como los números pueden ser sumados, restados, multiplicados o divididos, los términos algebraicos pueden ser operados de esta forma, pero, se requieren de ciertas condiciones algebraicas para esto. La condición algebraica principal, y la más básica, es la semejanza. Sin la semejanza no es posible hacer la operación aritmética más básica.

El mero hecho de hacer una comparación entre objetos trae consigo, irremediablemente, que se observen características similares y opuestas. Debes de saber que esta cuestión es también ineludible en el álgebra. Pero, de las dos facetas de la comparación la que cobra más relevancia es la semejanza, debido a que permite hallar simplificaciones y reducciones a extensos polinomios (y ecuaciones).

El elemento en común que se toma en cuenta en la semejanza de términos algebraicos es la parte literal. Si un par o grupo de términos poseen la parte literal, entonces, estos son semejantes.

La simplificación por medio de la semejanza de términos, es conocida en el álgebra como la reducción de términos semejantes. Esta es la simplificación elemental que permite sumar y restar términos algebraicos en polinomios.

Ejemplos de suma y resta de términos algebraicos

Para demostrarte el poder matemático de la reducción de términos semejantes, a continuación te mostraremos un par de ejemplos:

$6a-17b+c+22-88a+11b-23c+45$

Primero, conviene separar cada literal, operando a sus términos semejantes de la siguiente manera:

$6a-88a=-82a$
$-17b+11b=-6b$
$c-23c=-22c$

Y por último, sumamos a los coeficientes: $22+45=67$

Resultando el polinomio: $-82a-8b-22c+67$

$\frac{3xy^{2}}{4}+x^{2}y^{3}-6y+\frac{5xy^{2}}{6}-\frac{x^{2}y^{3}}{4}+11y-\frac{xy^{2}}{3}-2x^{2}y^{3}-\frac{5y}{2}$

Operando por separado:

$\frac{3xy^{2}}{4}+\frac{5xy^{2}}{6}-\frac{xy^{2}}{3}=\frac{5xy^{2}}{4}$
$x^{2}y^{3}-\frac{x^{2}y^{3}}{4}-2x^{2}y^{3}=-\frac{-5x^{2}y^{3}}{4}$
$-6y+11y-\frac{5y}{2}=\frac{5y}{2}$

Resultando:

$\frac{5xy^{2}}{4}-\frac{5x^{2}y^{3}}{4}+\frac{5y}{2}$

Ejercicios propuestos

Con el fin de afinar tus habilidades algebraicas, te dejamos algunos términos algebraicos siendo sumados y restados para que sean reducidos:

$a+2b-66c+99-3a+7b-27c-102$
$0,2a+0,5b+0,7c-0,8a-0,8b-0,09c-7a+8b-11c$
$\frac{a^{2}{3}-\frac{2b}{3}+3a^{2}+5b-\frac{3a^{2}}{7}+\frac{3b}{2}+99-192$
$0,5x^{2}y+333+\frac{2xy^{2}}{9}-0,88y^{3}+\frac{4x^{2}y}{7}-0,78xy^{2}+\frac{5y^{3}}{7}-77,8$