Algunas características de este conjunto numérico son: El conjunto de los números enteros 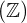está formado por: Los números enteros positivos 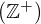: 1, 2, 3, … El cero: 0. Los números...
Blog de Matematicas
Números enteros
Números
Números enteros
Números enteros

Números enteros

Algunas características de este conjunto numérico son:

  1. El conjunto de los números enteros (\mathbb{Z}) está formado por:
    • Los números enteros positivos
      (\mathbb{Z}^{+}): 1, 2, 3, …
    • El cero: 0.
    • Los números enteros negativos
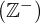      (\mathbb{Z}^{-}): -1 , – 2, – 3, …

    Todos estos números conforman el conjunto de los números enteros, el cual se denota por: 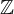\mathbb{Z} = { … , -4, – 3, – 2, -1, 0, 1, 2, 3, 4, … }.

  2. El conjunto de los números enteros es un conjunto ordenado, infinito y sin primer elemento.
  3. Los números enteros negativos se escriben con un signo (-) delante del número (para indicar que es menor que cero). Cuando un número distinto de cero no va precedido de ningún signo, se entiende que este es positivo.

Relación de orden

En el conjunto de los números enteros se pueden definir las mismas relaciones de orden que en los números naturales: menor que, mayor que o igual que. Es así que dado dos números enteros cualesquiera, siempre hay uno menor y otro mayor, salvo que ambos números sean iguales.

Signos para comparar

Para comparar números enteros se utilizan los mismos signos que para los números naturales.

Símbolos Ejemplos
< menor que. – 5 < 9, se lee «menos cinco es menor que nueve».
– 4 > – 7, se lee «menos cuatro es mayor que menos siete».
2 = 2, se lee «dos es igual que dos».
> mayor que.
= igual.
\leq menor o igual que.
\geq mayor o igual que.

Representación de los números enteros en la recta numérica

Los números enteros se representan de forma ordenada en una recta numérica.
Para representar un número entero en una recta:

  1. Se ubica el cero.
  2. Los números enteros positivos se ubican (a igual distancia unos de otros) a la derecha del cero.
  3. Los números enteros negativos se ubican (a igual distancia unos de otros) a la izquierda del cero.
  4. En una recta numérica, será mayor aquel número que se ubique más a la derecha.
Números enteros

Representación en la recta numérica del conjunto \;\; \mathbb{Z}.

Valor absoluto de un número entero

El valor absoluto de un número cualquiera corresponde a la distancia de dicho número al punto de origen o cero. Para representar el valor absoluto de un número se utilizan dos barritas verticales. Es decir, el valor absoluto de un número entero a se representa por \begin{vmatrix} 1 \end{vmatrix}.

Ejemplo:

\begin{vmatrix} 3 \end{vmatrix}, representa tres unidades de distancia al cero. Es decir, \begin{vmatrix} 3 \end{vmatrix} = 3.
\begin{vmatrix} -3 \end{vmatrix}, representa tres unidades de distancia al cero. Es decir, \begin{vmatrix} -3 \end{vmatrix} = 3.

Valor absoluto

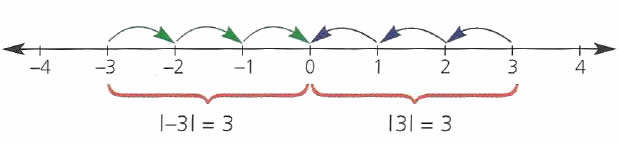
Los valores absolutos de – 3 y 3 son equivalentes, es decir, están a igual distancia del cero.

Valor absoluto de números opuestos

Si dos números tienen igual valor absoluto, pero distinto signo, se dice que estos números son opuestos. Ejemplo: – 5 y 5.

Propiedades en los números enteros

En el conjunto de los números enteros se definen habitualmente dos operaciones: la adición y la multiplicación.

Op. / Prop. Adición Multiplicación
Clausura Al sumar dos números enteros, su resultado también será un número entero.

    \[ \forall \;\; a\;\in \mathbb{Z} \;y\;\; \forall\;\;b\;\;\in \;\;\mathbb{Z}, \]

    \[ a+b=c, \;con \;\;c \;\in \; \mathbb{Z} \]

 Al multiplicar dos números enteros, su producto también será un número entero.

    \[ \forall \;\; a\;\in \mathbb{Z} \;y\;\; \forall\;\;b\;\;\in \;\;\mathbb{Z}, \]

    \[ a\cdot b=c, \;con \;\;c \;\in \; \mathbb{Z}$ \]
Conmutatividad

    \[ \forall \;\; a\;\in \mathbb{Z} \;y\;\; \forall\;\;b\;\;\in \;\;\mathbb{Z}, \]

    \[ a+b=b+a \]

    \[ \forall \;\; a\;\in \mathbb{Z} \;y\;\; \forall\;\;b\;\;\in \;\;\mathbb{Z}, \]

    \[ a\cdot b=b\cdota \]
Asociatividad

    \[ \forall \;\; a\;\in\;\; \mathbb{Z} \;,\;\; \forall\;\;b\;\in \;\;\mathbb{Z}\;\; y\;\;\forall \;\; c\;\in\;\; \mathbb{Z} \]

    \[ (a + b) + c = a + (b + c)\]

    \[ \forall \;\; a\;\in\;\; \mathbb{Z} \;,\;\; \forall\;\;b\;\in \;\;\mathbb{Z}\;\; y\;\;\forall \;\; c\;\in\;\; \mathbb{Z} \]

    \[ (a \cdot b) \cdot c= a\cdot (b\cdot c) \]
Elemento neutro

    \[ $\forall \;\; a\;\in\; \mathbb{Z},\exists \: 0\in\;\mathbb{Z}\; \;tal \;que \]

    \[ a + 0 = 0 + a = a \]

    \[ $\forall \;\; a\;\in\; \mathbb{Z},\exists \: 1\in\;\mathbb{Z}\; \;tal \;que \]

    \[ a\cdot 1=1\cdot a=a \]
Elemento inverso

    \[ $\forall \;\; a\;\in\; \mathbb{Z},\exists \: -a\in\;\mathbb{Z}\; \;tal \;que \]

    \[ a + (-a) = (-a) + a = 0 \]

 No se cumple.
Distributividad

    \[ \forall \;\; a\;\in\;\; \mathbb{Z} \;,\;\; \forall\;\;b\;\in \;\;\mathbb{Z}\;\; y\;\;\forall \;\; c\;\in\;\; \mathbb{Z},\; a\cdot (b+c)=a\cdot b+a\cdot c \]

Etiquetas:

Síguenos