Números racionales

El conjunto de los números racionales $(\mathbb{Q})$ está formado por todos los números que pueden ser escritos de la forma $\; \; \frac{a}{b}\; \;$ , tal que $a$ y $b$ son números enteros, con $b\neq 0$ .

Ejemplos:

$\frac{1}{3} \; \; \: \: \frac{4}{1} \; \; \: \:\frac{-9}{8}\; \; \: \:-1,08$

Características de los números racionales

$\mathbb{Q}$ es un conjunto infinito.
$\mathbb{Q}$ no tiene primer ni último elemento.
$\mathbb{Q}$ es un conjunto ordenado.
$\mathbb{Q}$ es un conjunto denso, es decir, entre dos números racionales existen infinitos números racionales.

Expresión fraccionaria

En una expresión de la forma: $\frac{a}{b}$ , el numerador es $a$ y el denominador es $b$ .

Amplificación y simplificación

Para amplificar una expresión de la forma $\frac{a}{b}$ se debe multiplicar por el mismo factor el numerador y el denominador.

Ejemplo:

$\frac{2}{3}=\frac{2\cdot 2}{3\cdot 2}= \frac{4}{6}$

Para simplificar una expresión de la forma $\frac{a}{b}$ se debe dividir el numerador y el denominador por el mismo número.

Ejemplo:

$\frac{8}{10}=\frac{8 : 2}{10: 2}= \frac{4}{5}$

Mediante la amplificación y la simplificación se pueden obtener distintos representantes de un número racional.

Representación de los números racionales

Cada número racional puede ser representado por infinitas expresiones fraccionarias equivalentes entre sí. Por ejemplo, el número racional $\; \; \frac{3}{4}\; \;$ puede ser representado por:

$\frac{-6}{-8},\; \; \frac{-3}{-4},\; \; \frac{3}{4},\; \; \frac{6}{8},\; \; \frac{9}{12},\; \; \frac{12}{16},\; \; ...$

Un conjunto de fracciones equivalentes representa un único número racional. Es decir, el número racional es el representante del conjunto de todas las fracciones equivalentes a una dada.

Representación de un número racional en la recta numérica

Para ubicar números racionales en una recta numérica se pueden seguir los siguientes pasos:

Se divide cada segmento que representa una unidad, en el número de partes iguales que indica el denominador.
A partir del cero, se cuenta el número de partes que indica el numerador. Esta ubicación indica la posición del número racional en la recta numérica.

Ejemplo: representar $-\frac{4}{3},\; \; \frac{2}{3}\; \; y\; \; \frac{7}{3}$

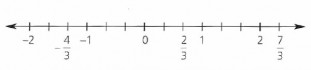
A cada número racional le corresponde un único punto en la recta numérica, pero no a todo punto de la recta numérica le corresponde un número racional, es decir, $\mathbb{Q}$ «no completa la recta numérica».